What is this diagram?
Let me give the most bare explanation of the diagram.
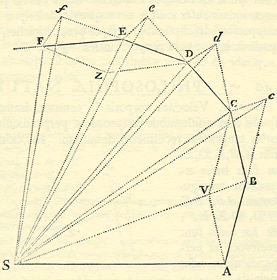
Consider the somewhat darker line running from A to B to C to D to E to F. This will represent the path of a body in motion from A to F.
Consider a body at A. If it is in motion and unaffected by anything else, it will move in a straight line—say, towards B. AB thus represents its motion under its own impetus.
Now consider point S as a center of force–like a magnet, or a large body exerting a gravitational force on another. Newton says: imagine that the body at A is acted on by S in such away that it is pulled toward S–again, the way that a magnet or body with gravitational force would. Now, the body at A is impelled by its own motion to move in a straight line from A to B to c. If there were no body affecting it at S, it would just keep going on that straight line from A to B to c until–- until it ran into something, or some other force affected it…
Now consider the effect of S on this body. Let us say that the effect of S acts instantaneously on the body when it hits B to draw it in from B to V. Then it would move from V to C, just as it would have from B to c–VC parallel to Bc and equal in length to it. This allows us to see C as the position that the body will actually take under the joint effect of its own motion and the force at S. The same will go for d and D etc–in each case, the miniscule letter shows where the body would have been if there had been no force at S, and the majuscule shows where it actually ends up.
Lastly, imagine that instead of six steps to get from A to F, we consider 100 steps—or a thousand. With each increase in the number of steps, the distance from one “stop” to another shrinks. Newton asks us to consider the motion (and the resulting path) when we shrink the distance between the stops down to nothing—“infinitesimally small.” The path gets closer and closer to a curve as these increments shrink.
Newton is simply asking us to imagine the orbit of a planet (or an electron) and helping us to understand what it means that that orbital motion could be due to the joint operation of two forces–a straight line force within the moving body, and another straight line force, acting on it at every instant, pulling it in toward itself.
The wonder of the proposition is not that Newton somehow demonstrates that planetary motion can be decomposed into two forces–that is not what the proposition demonstrates but what it assumes. The wonder of the proposition is how much he makes knowable about that motion. And he does it all by a kind of geometrical reasoning.
The proposition is dear to me and emblematic of the project for several reasons. The proposition and its diagram have a surface simplicity (so few points and lines, such elegant geometrical reasoning) yet it is impossible for me to master it. No matter how many times I return to it, it remains not only marvelous but nearly opaque. Winemaking has the same kind of marvelous opacity to me: one has glimpses into what is going on, one has moments of understanding; but what is going on is so immeasurably deep and complex that the glimpses remain punctuations at best. But it is nonetheless possible to follow Newton, even if it is impossible for me to master him. The same is true with the wine: there is something luminous and knowable going on, even if it is impossible to master it.
It is dear for another important reason too. When I was learning how to make wine, the son of my teacher and mentor was in the last few years of his home schooling. His academy was in need of a new faculty member to enliven the curriculum. John Kongsgaard proposed that as he was teaching me, I would teach his and Maggy's son Alex. It was a wonderful idea.
Alex and I met two to three times a week, for several hours at a time, some of them on the Vallejo-San Francisco ferry (carrying me back from work), some of them at my kitchen table. We did this for two school years, and studied everything from Beowulf to Genesis to Dashiell Hammett to Ancient Greek. But somehow at the center of everything for me was Newton. We spent a whole year studying Newton together, drawing obscure diagrams on the tables on the ferry, and the culmination of our whole year's study was being able to demonstrate this diagram, Proposition 1 of the Principia. Alex's final exam was a public demonstration before his parents on an easel in my kitchen, followed by dinner. Very soon, Alex was not only my student, but my friend, my helper in winemaking, and my teacher too.